Ma trận có một lịch sử dài về ứng dụng trong giải các phương trình tuyến tính nhưng chúng được biết đến là các mảng cho tới tận những năm 1800.
Nhà toán học người Anh Cullis là người đầu tiên sử dụng ký hiệu ngoặc hiện đại cho ma trận vào năm 1913 và ông cũng viết ra ký hiệu quan trọng A = [ai,j] để biểu diễn một ma trận với ai,j là phần tử ở hàng thứ i và cột thứ j.
Cauchy là người đầu tiên chứng minh những mệnh đề tổng quát về định thức, khi ông sử dụng định nghĩa như sau về định thức của ma trận A = [ai,j]: thay thế lũy thừa ajk bằng ajk trong đa thức.
Ma trận thường được viết trong dấu ngoặc vuông
Cộng hai ma trận:
Nhân (vô hướng) một số với ma trận
Chuyển vị
Nhân ma trận: Phép nhân hai ma trận được xác định khi và chỉ khi số cột của ma trận bên trái bằng số hàng của ma trận bên phải.
Ma trận con: Ma trận con của một ma trận nhận được bằng cách xóa bất kỳ các hàng và các cột. Ma trận con được ký hiệu là Mij với i là dòng bị xóa, j là cột bị xóa. Ví dụ, từ ma trận 3 x 4, chúng ta có thể tạo ra ma trận con 2x3 bằng cách xóa hàng 3 và cột 2:
Phương trình tuyến tính:
Hệ phương trình tuyến tính:
Biến đổi tuyến tính: Ma trận và phép nhân ma trận cho thấy những đặc điểm cơ bản của chúng khi liên hệ với biến đổi tuyến tính.
Ví dụ, ma trận vuông 2×2: có thể coi như là biến đổi của hình vuông đơn vị thành một hình bình hành với các đỉnh của nó nằm tại (0, 0), (a, b), (a + c, b + d), và (c, d)
Đối với bộ dữ liệu rất lớn, nhiều hàng nhiều cột. Việc áp dụng các kiến thức về ma trận là một công cụ vô cùng mạnh mẽ giúp xử lý số liệu nhanh chóng và chính xác. Numpy (Numeric Python): là một thư viện toán học phổ biến và mạnh mẽ của Python. Cho phép làm việc hiệu quả với ma trận và mảng, đặc biệt là dữ liệu ma trận và mảng lớn với tốc độ xử lý nhanh.
Cài đặt thư viện Numpy : Mở Command Prompt và gõ lệnh: pip install numpy
Khai báo thư viện : import numpy as np
# Ma trận A là một bảng dữ liệu gồm m hàng và n cột.
# Trong Numpy, người ta dùng một mảng ndarray hai chiều để biểu diễn một ma trận.
# Hay nói cách khác, ma trận trong Numpy là mảng của các vecto một chiều thông thường.
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(arr)
kết quả:
[[1 2 3]
[4 5 6]
[7 8 9]]
print(arr[1, 2])
6
arr = np.array([[1, 2, 3, 4], [4, 5, 6, 7], [7, 8, 9, 10]])
# Để trả về kích cỡ của ma trận, ta dùng hàm shape. Cần chú ý rằng kiểu dữ liệu trả về ở đây là tuples.
print(arr.shape)
A = np.array([[1, 3, 4], [-2, 6, 0], [-5, 7, 2]])
B = np.array([[2, 3, 4], [-1, -2, -3], [0, 4, -4]])
print("A + B = \n", A + B)
print("A - B = \n", A - B)
kết quả:
A + B =
[[ 3 6 8]
[-3 4 -3]
[-5 11 -2]]
A - B =
[[-1 0 0]
[-1 8 3]
[-5 3 6]]
# Phép nhân/ chia ma trận với một số
print("A * 3 = \n", A * 3)
print("A / 4 = \n", A / 4)
A * 3 =
[[ 3 9 12]
[ -6 18 0]
[-15 21 6]]
A / 4 =
[[ 0.25 0.75 1. ]
[-0.5 1.5 0. ]
[-1.25 1.75 0.5 ]]
# Phép nhân hai ma trận
# Ta cần chú ý rằng thứ tự của phép nhân hai ma trận rất quan trọng,
# chỉ có thể thực hiện được nếu số cột của ma trận thứ nhất bằng số hàng của ma trận thứ hai
# Trong Numpy, ta có thể dùng toán tử @ tiến hành nhân hai ma trận
print("A * B = \n", A @ B)
print("B * A = \n", B @ A)
A * B =
[[ -1 13 -21]
[-10 -18 -26]
[-17 -21 -49]]
B * A =
[[-24 52 16]
[ 18 -36 -10]
[ 12 -4 -8]]
# Ta thử khai báo một ma trận đơn vị cấp 3 trong Numpy như sau:
arr = np.eye(3)
print(arr)
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
# Ma trận đường chéo
# là ma trận vuông cấp n thỏa mãn mọi phần tử không nằm trên đường chéo chính đều bằng 0
A = np.diag([1, 2, 3])
print(A)
[[1 0 0]
[0 2 0]
[0 0 3]]
# Ma trận chuyển vị
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(A.T)
[[1 0 0]
[0 2 0]
[0 0 3]]
Các hàm thống kê
arr.max() hoặc np.max(arr): Lấy giá trị lớn nhất của mảng arr.
arr.min() hoặc np.min(arr): Lấy giá trị nhỏ nhất của mảng arr.
arr.sum() hoặc np.sum(arr): Tổng tất cả các phần tử trong mảng arr.
arr.mean() hoặc np.mean(arr): Trung bình cộng của tất cả các phần tử trong mảng arr.
np.median(arr): Trả về giá trị trung vị của mảng arr.
print("Giá trị lớn nhất của mảng arr là:", np.max(arr))
print("Giá trị nhỏ nhất của mảng arr là:", np.min(arr))
print("Tổng tất cả các phần tử của mảng arr là:", np.sum(arr))
print("Trung bình cộng tất cả các phần tử của mảng arr là:", np.mean(arr))
print("Giá trị trung vị của mảng arr là:", np.median(arr))
###### Chèn giá trị vào trước cột/hàng được chỉ định ######
a1 = np.array([[1, 1], [2, 2], [3, 3]]) print (np.insert(a1, 1, 5)) # [1 5 1 2 2 3 3]
a1 = np.array([[1, 1], [2, 2], [3, 3]]) print (np.insert(a1, 3, 2)) |
# chèn vào cột print (np.insert(a1, 1, 5, axis=1)) [[1 5 1]
[2 5 2]
[3 5 3]] |
# chèn vào hàng |
print (np.insert(a1, 1, 5, axis=0)) [[1 1]
[5 5]
[2 2]
[3 3]]
|

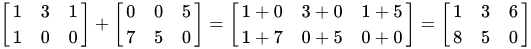

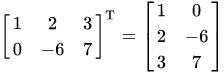

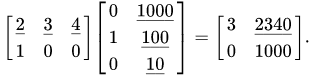


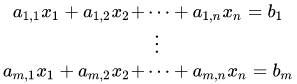




Nhận xét
Đăng nhận xét